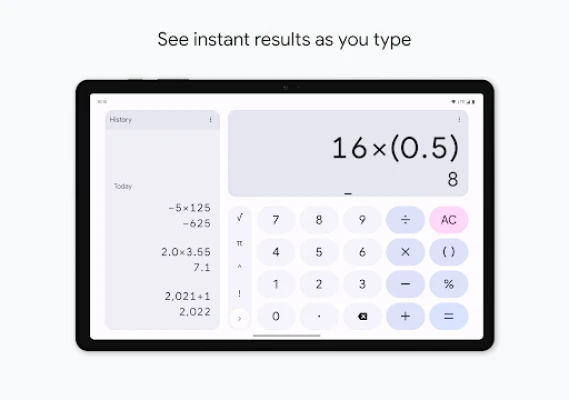
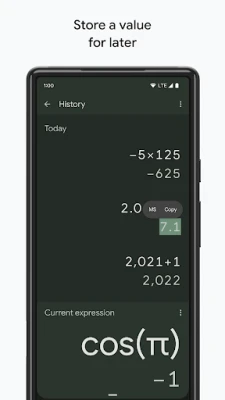
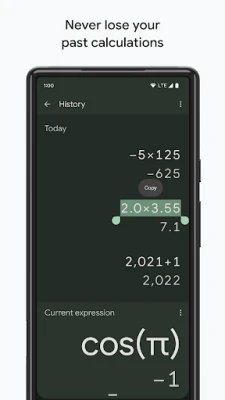
Latest Version
8.6.1 (625857114)
April 21, 2025
Google LLC
Tools
Android
0
Free
com.google.android.calculator
Report a Problem
More About Calculator
Mastering Basic and Scientific Calculations: A Comprehensive Guide
In today's fast-paced world, the ability to perform both basic and scientific calculations is essential. Whether you're a student, a professional, or simply someone who enjoys solving problems, understanding these mathematical operations can significantly enhance your analytical skills. This article will delve into the fundamental calculations and explore the more complex scientific operations that can elevate your mathematical prowess.
Understanding Basic Calculations
Basic calculations form the foundation of mathematics. They include four primary operations: addition, subtraction, multiplication, and division. Mastering these operations is crucial for everyday problem-solving and more advanced mathematical concepts.
Addition: The Foundation of Mathematics
Addition is the process of combining two or more numbers to obtain a sum. It is one of the first operations learned in mathematics and is used in various real-life situations, from budgeting to cooking. For example, if you have 5 apples and you buy 3 more, you now have a total of 8 apples:
5 + 3 = 8Subtraction: Finding the Difference
Subtraction involves taking one number away from another to find the difference. This operation is equally important, as it helps in understanding how quantities relate to one another. For instance, if you have 10 dollars and spend 4 dollars, you can calculate your remaining balance:
10 - 4 = 6Multiplication: Repeated Addition
Multiplication can be viewed as repeated addition. It allows you to quickly calculate the total of equal groups. For example, if you have 4 bags with 3 oranges each, you can find the total number of oranges by multiplying:
4 × 3 = 12Division: Splitting into Equal Parts
Division is the process of splitting a number into equal parts. It is the inverse of multiplication and is essential for understanding ratios and proportions. For instance, if you have 12 cookies and want to share them equally among 4 friends, you can determine how many cookies each friend receives:
12 ÷ 4 = 3Exploring Scientific Operations
Once you have a firm grasp of basic calculations, you can advance to scientific operations. These include trigonometric, logarithmic, and exponential functions, which are vital in various fields such as engineering, physics, and computer science.
Trigonometric Functions: Understanding Angles
Trigonometric functions relate the angles of a triangle to the lengths of its sides. The primary functions include sine (sin), cosine (cos), and tangent (tan). These functions are crucial in fields such as architecture and navigation. For example, if you know the angle of elevation and the distance from a point to the base of a building, you can calculate the height of the building using the sine function:
height = distance × sin(angle)Logarithmic Functions: The Inverse of Exponentiation
Logarithmic functions are the inverse of exponential functions. They help in solving equations where the unknown appears as an exponent. For instance, if you want to find out how many times you need to multiply 2 to get 16, you can use logarithms:
log₂(16) = 4This means that 2 raised to the power of 4 equals 16.
Exponential Functions: Growth and Decay
Exponential functions describe processes that grow or decay at a constant rate. They are commonly used in finance, biology, and physics. For example, if you invest money in a bank account with a fixed interest rate, the amount of money grows exponentially over time. The formula for exponential growth is:
A = P(1 + r)ⁿWhere:
- A = the amount of money accumulated after n years, including interest.
- P = the principal amount (the initial amount of money).
- r = the annual interest rate (decimal).
- n = the number of years the money is invested or borrowed.
Practical Applications of Calculations
Understanding both basic and scientific calculations has numerous practical applications. Here are a few examples:
- Finance: Budgeting, calculating interest rates, and analyzing investments all require a solid understanding of mathematical operations.
- Engineering: Engineers use trigonometric functions to design structures and analyze forces.
- Science: Logarithmic and exponential functions are essential in fields like biology for modeling population growth and decay.
Conclusion
Mastering basic and scientific calculations is not just an academic exercise; it is a vital skill that can enhance your problem-solving abilities in everyday life and professional settings. By understanding addition, subtraction, multiplication, and division, as well as delving into trigonometric, logarithmic, and exponential functions, you equip yourself with the tools necessary to tackle a wide range of challenges. Embrace these mathematical concepts, and watch as they empower you to make informed decisions and solve complex problems with confidence.
Rate the App
User Reviews
Popular Apps










Editor's Choice