Mastering Mathematics: Your Ultimate Guide to Solving Integrals, Derivatives, and More

Mathematics can often feel overwhelming, especially when tackling complex topics such as integrals, derivatives, limits, and trigonometry. However, with the right tools and resources, students can navigate these challenges with confidence. This article explores essential mathematical concepts and introduces a powerful tool designed to assist high school and college students, teachers, and parents in mastering these subjects.

Understanding Key Mathematical Concepts

Mathematics encompasses a wide range of topics, each with its own set of rules and applications. Here, we break down some of the fundamental areas that students often encounter:

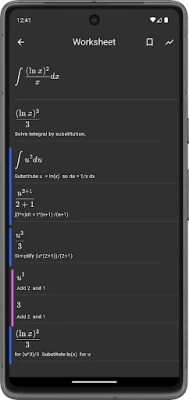
1. Integrals

Integrals are a core component of calculus, representing the accumulation of quantities. They are essential for calculating areas under curves and solving problems related to rates of change. Understanding both definite and indefinite integrals is crucial for students aiming to excel in calculus.

2. Derivatives

Derivatives measure how a function changes as its input changes. They are vital for understanding motion, optimization, and various real-world applications. Mastering the rules of differentiation, including the product, quotient, and chain rules, is essential for success in calculus.

3. Limits

Limits are foundational to calculus, helping to define both derivatives and integrals. They allow students to understand the behavior of functions as they approach specific points or infinity. Grasping the concept of limits is crucial for tackling more advanced topics in mathematics.

4. Trigonometry

Trigonometry focuses on the relationships between the angles and sides of triangles. It is essential for various applications in physics, engineering, and architecture. Key concepts include sine, cosine, tangent, and their inverses, as well as the unit circle.

5. Logarithms

Logarithms are the inverse operations of exponentiation and are crucial for solving exponential equations. Understanding the properties of logarithms, including the product, quotient, and power rules, is vital for students working with complex equations.

6. Equations

Equations are mathematical statements that assert the equality of two expressions. Solving equations is a fundamental skill in mathematics, encompassing linear, quadratic, and polynomial equations. Mastery of these concepts is essential for progressing in algebra and beyond.

7. Algebra

Algebra serves as the foundation for higher-level mathematics. It involves manipulating symbols and solving for unknowns. Key topics include simplifying expressions, solving equations, and working with inequalities.

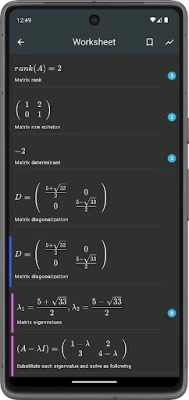
8. Linear Algebra: Matrices and Vectors

Linear algebra focuses on vector spaces and linear mappings between them. It is essential for understanding systems of equations, transformations, and more. Students should familiarize themselves with matrices, determinants, and eigenvalues to excel in this area.

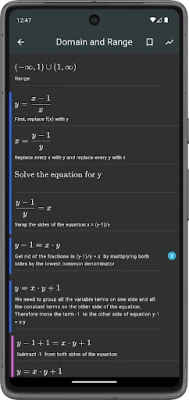
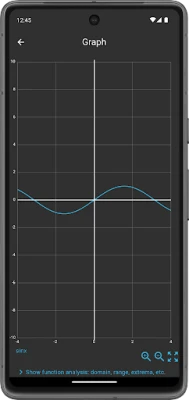
9. Function Analysis: Domain, Range, Extrema, and Concavity

Function analysis involves studying the properties of functions, including their domain and range, as well as identifying extrema and concavity. This knowledge is crucial for graphing functions and understanding their behavior.

How MalMath Can Help You Succeed

For students struggling with these mathematical concepts, MalMath offers a comprehensive solution. This innovative tool provides a range of features designed to enhance understanding and improve problem-solving skills:

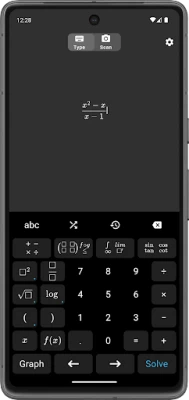
• Step-by-Step Descriptions: MalMath breaks down complex problems into manageable steps, providing detailed explanations for each stage of the solution process.
• Visual Highlights: The tool uses visual aids to make the steps easier to understand, helping students grasp concepts more effectively.
• Graph Analysis: MalMath includes graphing capabilities, allowing students to visualize functions and their properties.
• Problem Generation: The platform generates math problems across various categories and difficulty levels, providing ample practice opportunities.
• Save and Share Solutions: Students can save their solutions and graphs for future reference or share them with peers and teachers.

Available Languages

MalMath is accessible in multiple languages, including:

• English
• German
• Spanish
• Italian
• French
• Turkish
• Albanian
• Croatian
• Arabic
• Portuguese
• Azerbaijani
• Russian
• Japanese

Conclusion

Mathematics is a vital skill that opens doors to numerous academic and professional opportunities. By mastering key concepts such as integrals, derivatives, limits, and more, students can build a strong foundation for future success. With the help of tools like MalMath, understanding and solving complex mathematical problems becomes an achievable goal. Explore more about MalMath and enhance your mathematical journey at MalMath.com.